继上篇KMP、BM算法(上),这篇中的BM算法比KMP算法的效率更高,构思精巧。但是算法实现起来也更困难,更难以理解。

可以先简单了解大概思想:阮一峰 http://www.ruanyifeng.com/blog/2013/05/boyer-moore_string_search_algorithm.html
一:算法思想:
图片转载来自 Alexia http://www.cnblogs.com/lanxuezaipiao/p/3452579.html
前提:假设文本串text长度为n,模式串pattern长度为m,从右走往左匹配
1、
- 第一步,将pattern 从右往左匹配,发现最后一个字符 c 与 d 不匹配。我们称这样不匹配的字符为“坏字符”(text 红色)。而且 pattern 中并没有 d ,于是我们知道需将 pattern 右移长度m 即 5 以重新匹配。(右移1、2、3、4也不会匹配,聪明的你肯定想到了)
- 现在到达 BM 行位置,再从右往左匹配,发现最后一个字符 c 与 b 不匹配。对的,这个时候 b 就是“坏字符”。然而这pattern 中包含了 b ,我们就可以直接将pattern 移动到其中的 b与“坏字符”对应的位置(聪明的你肯定看出来了),但是pattern 中有两个 b,移动就需要选择近的那个避免漏掉。
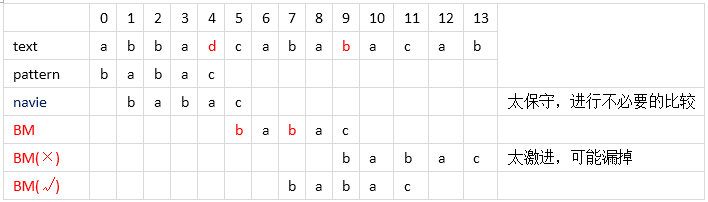
2、在继续前面的移动后,可以看到在BM行中从右到左匹配,符合匹配的依次是c、a、b 但是之后发现pattern 中的a 并不匹配 b。如果这时依然使用之前的策略,将其移动到 之后对应的b 的位置,反而走了回头路,这样我们就需要将pattern 右移一步。这就是其中的“坏字符”算法思想
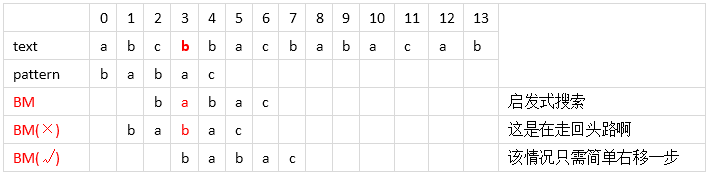
3、
- 再接着看下面,在使用一次“坏字符”算法后,BM 行从右往左发现 pattern 中依次为 b、a是匹配的,之后 b不匹配 a时,运用上面的“坏字符”算法,我们可以右移一位。(这样当然也可以)
- 但是这次,我们需要利用起已经匹配的 “ab” 两个字符,就叫它“好后缀”。在pattern 中发现在其中有和“好后缀”匹配的 “ab”,于是我们就可以将pattern 右移使得其对应的位置。这就是其中的“好后缀” 算法思想
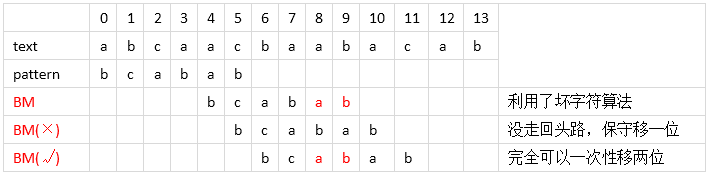
4、
- 接着看下面这个,在使用一次“坏字符”算法后,BM 行从右往左发现 pattern 中依次为 c、a、b是匹配的,之后 a 不匹配 b时,”bac” 是 “好后缀”,但是pattern 中并没有和其相匹配的其他串了,这时我们再用回“坏字符”算法”,但是又得注意不往左移动。(再怎么拼凑,左移注定没有意义的)

这便是BM算法中核心的两个算法思想:“坏字符”和“好后缀”算法。BM算法中,每一步的移动步数就是这两种算法中的最大值。
二:算法情况探讨:
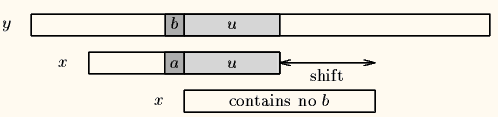
(1)坏字符算法
当出现一个坏字符时, BM算法向右移动模式串, 让模式串中最靠右的对应字符与坏字符相对,然后继续匹配。坏字符算法有两种情况。(为什么是最靠右?往最靠右相对不是有左移的情况吗?是的,但这由第二个算法限制它不左移动,别急)
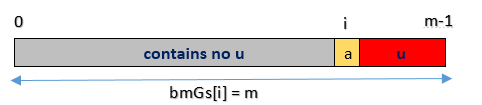
y 为文本串,x 为模式串,shift 为移动步数,u 有已匹配的串。
情况一:
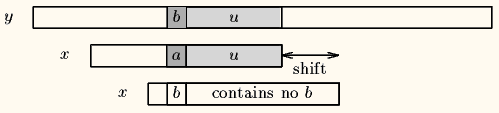
情况二:
(2)好后缀算法
情况一:模式串中有子串和好后缀完全匹配,则将最靠右的那个子串移动到好后缀的位置继续进行匹配。
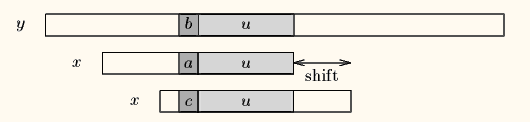
情况二:如果不存在和好后缀完全匹配的子串,则在好后缀中找到具有如下特征的最长子串,使得P[m-s…m]=P[0…s]。(P[]为pattern )
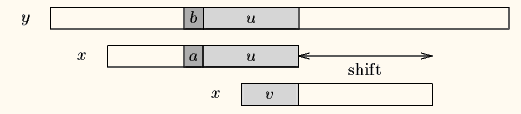
情况三:如果完全不存在和好后缀匹配的子串,则右移整个模式串。shift=m。
BM算法中,每一步的向右移动的步数都是这两种算法中的最大值。(不往左移动)
三:算法实现:
使用坏字符算法计算pattern需要右移的距离,存放在bmBc[],而按好后缀算法计算pattern右移的距离则要存放在bmGs[]。下面讲下怎么计算bmBc[]和bmGs[]这两个预处理数组。
(1)计算数组bmBc[ ]:
我们使用字符作为下标而不是位置数字作为下标。bmBc[字符] 对应的数组值即是该字符离pattern 最右端的距离,但如果是纯8位字符也只需要256个空间大小,而且对于大模式,可能本身长度就超过了256,所以这样做是值得的(这也是为什么数据越大,BM算法越高效的原因之一)。
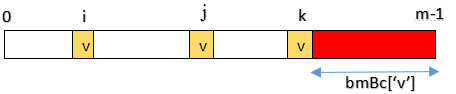
bmBc[]的计算分两种情况,与前一一对应。
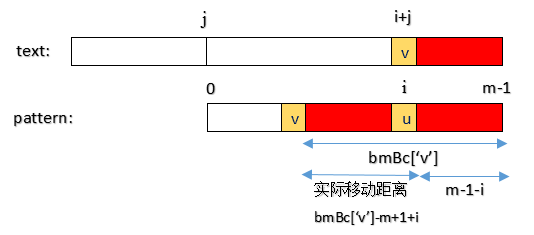
情况一:字符在模式串中有出现,bmBc[‘v’]表示字符v在模式串中最后一次出现的位置,距离模式串串尾的长度,如上图所示。
情况二:字符在模式串中没有出现,如模式串中没有字符v,则bmBc[‘v’] = strlen(pattern)。
写成代码也非常简单:
void PreBmBc(char *pattern, int m, int bmBc[])
{
int i;
for(i = 0; i < 256; i++)
bmBc[i] = m;
for(i = 0; i < m - 1; i++)//i<m-1避免bmBc[m-1]=0
bmBc[pattern[i]] = m - 1 - i;
}
图中v是text中的坏字符(对应位置i+j),在pattern中对应不匹配的位置为i,那么pattern实际要右移的距离就是:bmBc[‘v’] - m + 1 + i。(没错可能为负数)
(2)计算bmGs[ ]数组
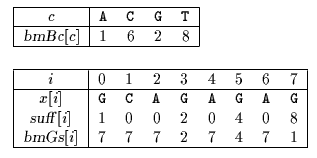
这里的bmGs[]的下标,是数字而不是字符了,是字符在pattern中位置,bmGs[ i ]应表示在 pattern 中当“好后缀”前不匹配位置在i 时,模式串应移动的距离。假设好后缀长度用数组suff[ ]表示。我们需要先把这个辅助数组suff[ ]求出。
而数组suff[ i ]表示pattern中以 i 位置字符为后缀和以最后一个字符为后缀的公共后缀串的长度。(好吧,需要举一个栗子)
suffix[m-1] = m;//m为pattern长度
suffix[i] = k
for [ pattern[i-k+1] ....,pattern[i]] == [pattern[m-1-k+1],pattern[m-1]]
i : 0 1 2 3 4 5 6 7
pattern: b c a b a b a b
- 当i=7时,按定义suff[7] = strlen(pattern) = 8
- 当i=6时,以pattern[6]为后缀的后缀串为bcababa,以最后一个字符b为后缀的后缀串为bcababab,两者没有公共后缀串,所以suff[6] = 0
- 当i=5时,以pattern[5]为后缀的后缀串为bcabab,以最后一个字符b为后缀的后缀串为bcababab,两者的公共后缀串为abab,所以suff[5] = 4
- 以此类推,当i=0时,以pattern[0]为后缀的后缀串为b,以最后一个字符b为后缀的后缀串为bcababab,两者的公共后缀串为b,所以suff[0] = 1
void suffix(char *pattern, int m, int suff[])\\生成suff[ ]数组 { int i,j; suff[m - 1] = m; for(i = m - 2; i >= 0; i--) { j = i; while(j >= 0 && pattern[j] == pattern[m - 1 - i + j]) j--; suff[i] = i - j; } }另一种改进算法就是利用了已经得到的suff[ ]值,计算现在正在计算的suff[]值。
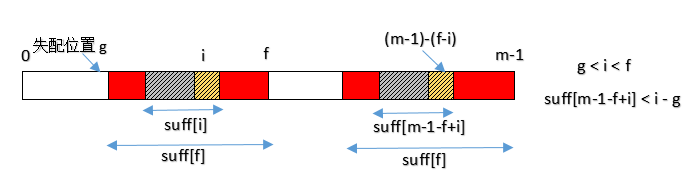
i 是当前正准备计算suff[]值的那个位置。f 是上一个成功进行匹配的起始位置。g 是上一次进行成功匹配的失配位置。
若 i 在 g 和 f 之间,那么一定有P[i]=P[m-1-f+i](P[ ]为pattern);并且如果suff[m-1-f+i] < i-g, 则suff[i] = suff[m-1-f+i],这不就利用了前面的suff了吗。(难以理解需中再熟悉suff[ ]定义)
void suffixes(char *x, int m, int *suff) {
int f, g, i;
suff[m - 1] = m;
g = m - 1;
for (i = m - 2; i >= 0; --i) {
if (i > g && suff[i + m - 1 - f] < i - g)
suff[i] = suff[i + m - 1 - f];
else {
if (i < g)
g = i;
f = i;
while (g >= 0 && x[g] == x[g + m - 1 - f])
--g;
suff[i] = f - g;
}
}
}
求出辅助数组suff[ ]后,再来讨论号后缀的几种情况中bmGs[ ]的值。
情况一: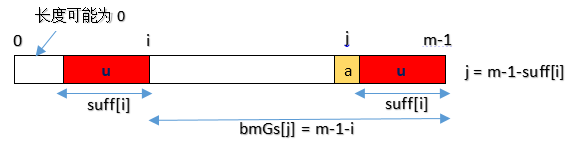
情况二:
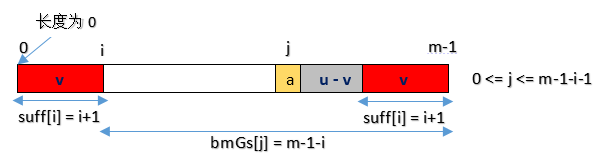
情况三:
void preBmGs(char *x, int m, int bmGs[]) {
int i, j, suff[XSIZE];
suffixes(x, m, suff);//计算suff[ ]
for (i = 0; i < m; ++i)//情况三
bmGs[i] = m;
j = 0;
for (i = m - 1; i >= 0; --i)//情况二
for (; j < m - 1 - i; ++j)
if (bmGs[j] == m)
bmGs[j] = m - 1 - i;
for (i = 0; i <= m - 2; ++i)//情况一
bmGs[m - 1 - suff[i]] = m - 1 - i;
}
再举一个栗子:
//完整代码
#include <stdio.h>
#include <string.h>
#define SIZE 256
#define MAX(x, y) (x) > (y) ? (x) : (y)
#define ASIZE 256
#define XSIZE 256
void BoyerMoore(char *pattern, int m, char *text, int n);
int main()
{
char text[256], pattern[256];
while(1)
{
scanf("%s%s", text, pattern);
if(text == 0 || pattern == 0) break;
BoyerMoore(pattern, strlen(pattern), text, strlen(text));
}
return 0;
}
void preBmBc(char *x, int m, int bmBc[]){
// void PreBmBc(char *pattern, int m, int bmBc[]) {
int i;
for (i = 0; i < ASIZE; ++i)
bmBc[i] = m;
for (i = 0; i < m - 1; ++i)
bmBc[x[i]] = m - i - 1;
}
void suffixes(char *x, int m, int *suff) {
int f, g, i;
suff[m - 1] = m;
g = m - 1;
for (i = m - 2; i >= 0; --i) {
if (i > g && suff[i + m - 1 - f] < i - g)
suff[i] = suff[i + m - 1 - f];
else {
if (i < g)
g = i;
f = i;
while (g >= 0 && x[g] == x[g + m - 1 - f])
--g;
suff[i] = f - g;
}
}
}
void preBmGs(char *x, int m, int bmGs[]) {
int i, j, suff[XSIZE];
suffixes(x, m, suff);
for (i = 0; i < m; ++i)
bmGs[i] = m;
j = 0;
for (i = m - 1; i >= 0; --i)
if (suff[i] == i + 1)
for (; j < m - 1 - i; ++j)
if (bmGs[j] == m)
bmGs[j] = m - 1 - i;
for (i = 0; i <= m - 2; ++i)
bmGs[m - 1 - suff[i]] = m - 1 - i;
}
void BoyerMoore(char *pattern, int m, char *text, int n)
{
int i, j, bmBc[ASIZE], bmGs[XSIZE];
// Preprocessing
preBmBc(pattern, m, bmBc);
preBmGs(pattern, m, bmGs);
// Searching
j = 0;
while(j <= n - m)
{
for(i = m - 1; i >= 0 && pattern[i] == text[i + j]; i--);
if(i < 0)
{
printf("The position is %d\n", j);
j += bmGs[0];
return;
}
else
{
j += MAX(bmBc[text[i + j]] - m + 1 + i, bmGs[i]);
}
}
printf("No find.\n");
}
参考资料:
Boyer-Moore algorithm http://igm.univ-mlv.fr/~lecroq/string/node14.html
Alexia(minmin) http://www.cnblogs.com/lanxuezaipiao/p/3452579.html
阮一峰 http://www.ruanyifeng.com/blog/2013/05/boyer-moore_string_search_algorithm.html